資訊內(nèi)容
【編程 | scratch】[02] 巧用scratch畫正多邊形
看了上次的scratch入門文章后,是不是感覺躍躍欲試了,上次我們體驗了scratch的畫筆功能,那我們今天就嘗試下用畫筆來畫幾何圖形吧。
上次用了畫筆工具后,編者興致盎然,一直想著用畫筆工具畫點什么?
本來想畫個三角形或正方形之類的,沒想到一發(fā)不可收拾,畫了很多很多正多邊形出來了,大家來欣賞下吧。
為了追求視覺上的統(tǒng)一,看起來沒那么雜亂,干脆在同一個圓內(nèi)畫了這么多正多邊形。不過雖然看著很簡單,可是對小學(xué)生來說,實現(xiàn)起來可能還有點難度,因為這里面用到了若干三角函數(shù)的基礎(chǔ)知識。
我們先不管上面的視頻,我們先想想,如果要畫個正方形,我們要怎么做呢?
畫正方形如果只畫個小正方形的話,可能很簡單。
畫之前特意問了我家的小朋友,小朋友只是說正方形方方正正的,四條邊一樣長。
方方正正是個什么意思呢?用稍微書面點的文字來描述,正方形主要有兩點性質(zhì):
-
正方形有四條等長的邊
-
正方形的每個角是直角
當我們用scratch畫正方形的時候,就會牽涉到下面兩個問題:
-
連續(xù)畫4條線段
-
連續(xù)的2條線段是互相垂直的(直角)
?
“落筆”開始畫
回憶下上節(jié)課的內(nèi)容,我們用畫筆工具畫線段的時候,是不是先要拿起畫筆往“舞臺區(qū)”上“落筆”呢?
如果我們不能確定“落筆”是什么意思,可以右擊“落筆”按鈕,然后再點擊旁邊所彈出的“幫助”按鈕,會看到“腳本區(qū)”上面會打開一個頁面,彈出如下提示和示例:
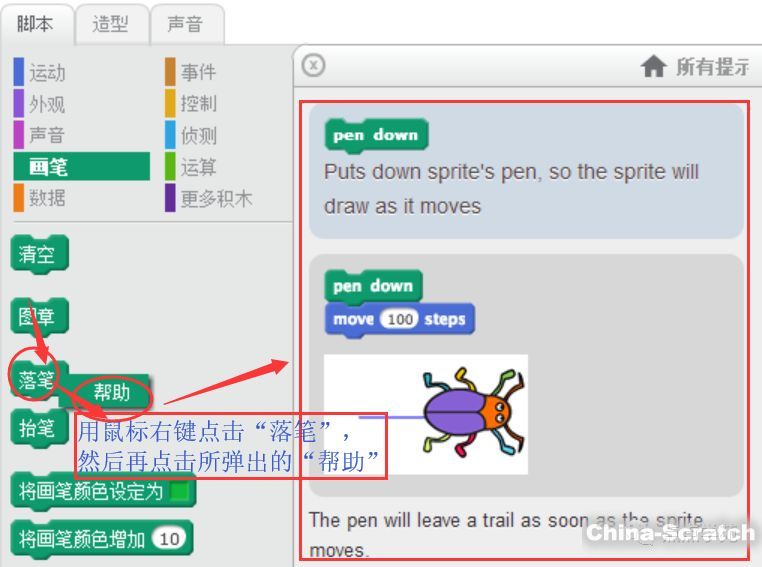
沒錯吧,“落筆”后再移動100步,小蟲子后面就會畫出一條線段。
?
畫線段
依樣畫葫蘆,我們也這樣搞,看看能不能畫出一條線段呢?
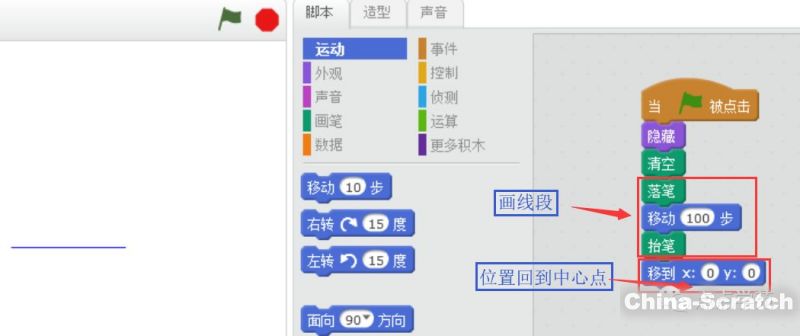
看到?jīng)]有,當我們點擊“旗幟”運行的時候,左邊“舞臺區(qū)”就畫上了一條藍色的線段。畫完以后我們“抬筆”,畫筆抬起來了,表示畫完了。
最后的“移到x:0 y:0”表示畫筆放回中心點,方便下次用。當然,還可以防止畫筆跑出了“舞臺區(qū)”。
?
畫直角
我們按照上面的方法,連續(xù)畫2條線段,2條線段之間形成一個夾角,怎么確保夾角是90度呢?
這里牽涉到角度的問題,小學(xué)低年級的小朋友可能還不知道轉(zhuǎn)一圈是360度,360度四等分成4個直角,每個直角就是90度。
我們知道了直角是90度后,用“運動模塊”里的右轉(zhuǎn)/左轉(zhuǎn)工具轉(zhuǎn)個90度再畫第2條線段,那這連續(xù)的2條線段形成的夾角就是直角。
我們調(diào)整下腳本。
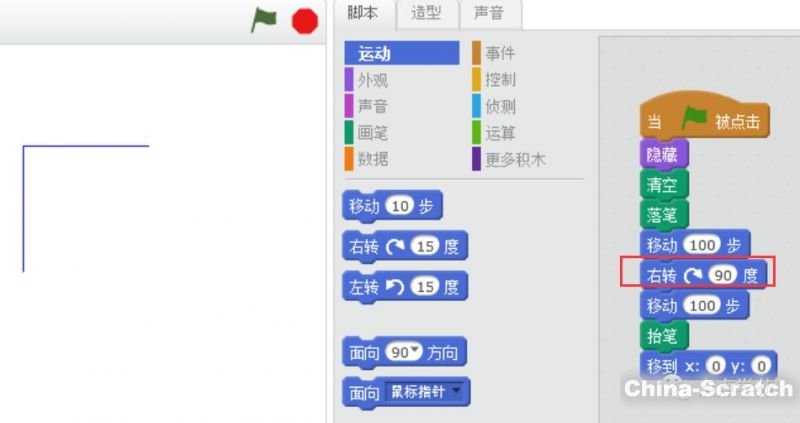
哈哈,直角搞定了。
?
重復(fù)右轉(zhuǎn)4次搞定正方形
那我們再繼續(xù)轉(zhuǎn)幾次正方形不就搞定了?
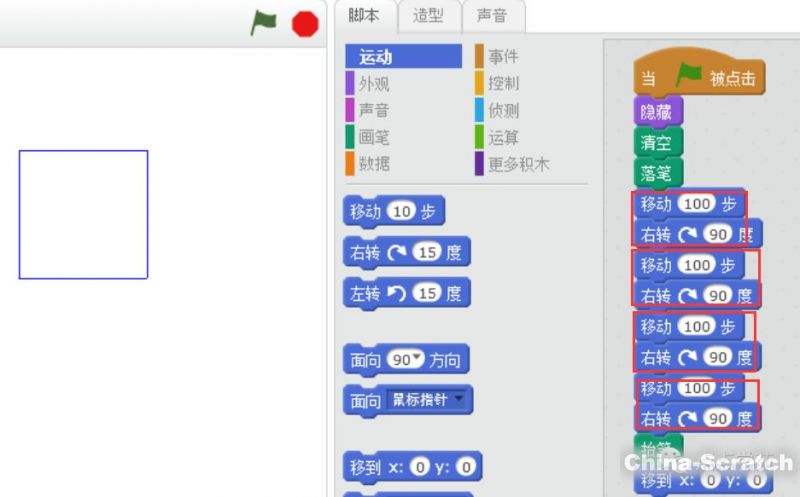
?
利用循環(huán)控制來簡化腳本
這樣雖然搞定了,但腳本看起來有點重復(fù),腳本里的移動100步都用了4次,還記得“控制”模塊里的“重復(fù)執(zhí)行”功能嗎?我們用它來精簡下。
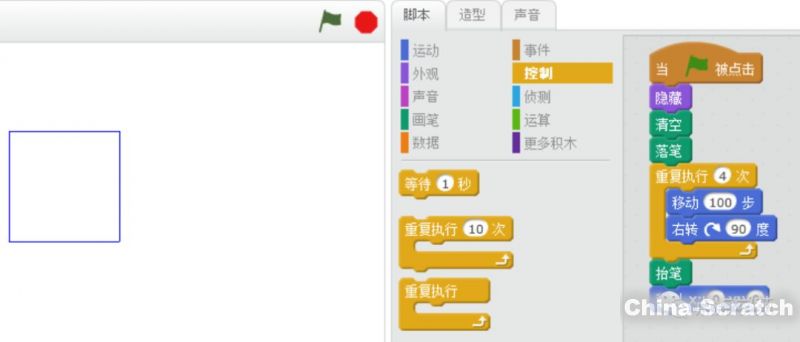
看起來是不是精簡些了呢?
畫個三角形?正方形搞定了,我們嘗試來畫個正三角形吧?!
和前面的區(qū)別,主要就是轉(zhuǎn)向的角度不一樣了吧,正方形是轉(zhuǎn)90度,三角形應(yīng)該轉(zhuǎn)多少度呢?
?
三角形的性質(zhì)
正三角形有哪些特性呢:
-
三條邊相等
-
三角形內(nèi)角和是180度,正三角形每個角是60度
那我們連續(xù)畫線段的時候,是不是每次轉(zhuǎn)個60度,回到起點后,就把一個正三角形畫好了呢?
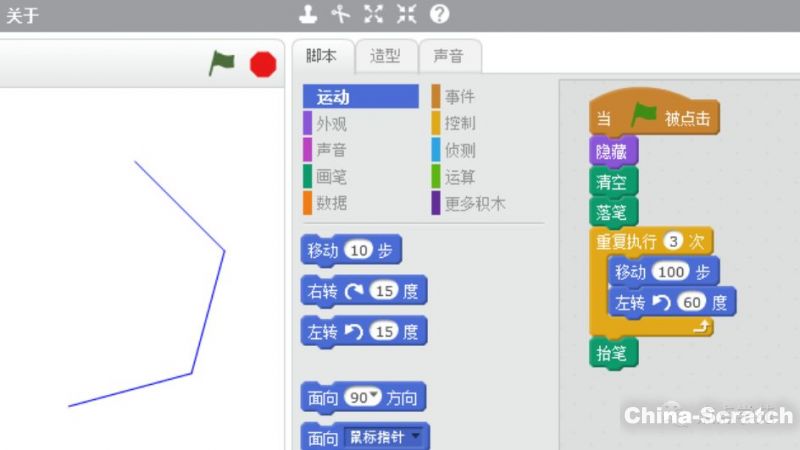
oh,my god!說好的三角形呢,怎么變成連續(xù)的幾條線段呢?不過線段看起來很有規(guī)律的,我們再多重復(fù)畫幾條試試吧。
?
失敗的三角形=六邊形
明明我們想畫個正三角形,可是畫出來的偏偏是個正六邊形?
想想,哪里搞錯了呢?原來呀,是我們的角度轉(zhuǎn)得不對。
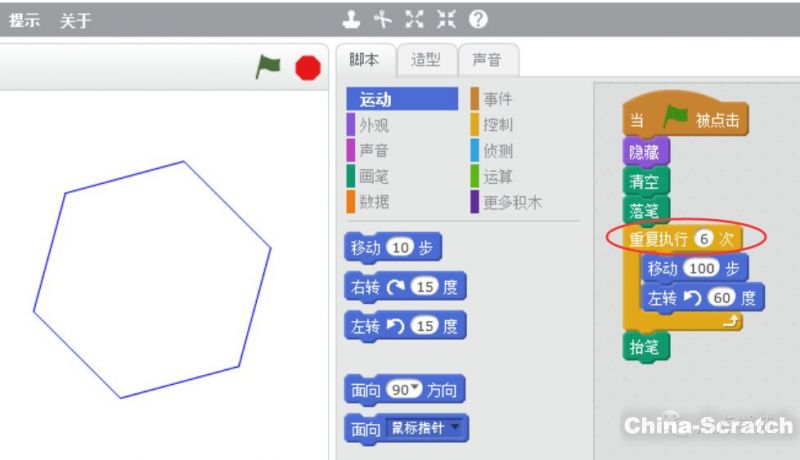
真是無心插柳柳成蔭啊,我們明明想畫個正三角形,因為方向轉(zhuǎn)錯了,竟然畫出個正六邊形出來了。
其實啊,如果左轉(zhuǎn)120度(和右轉(zhuǎn)60度等價),畫出來的就是正三角形了吧。
?
正十二邊形
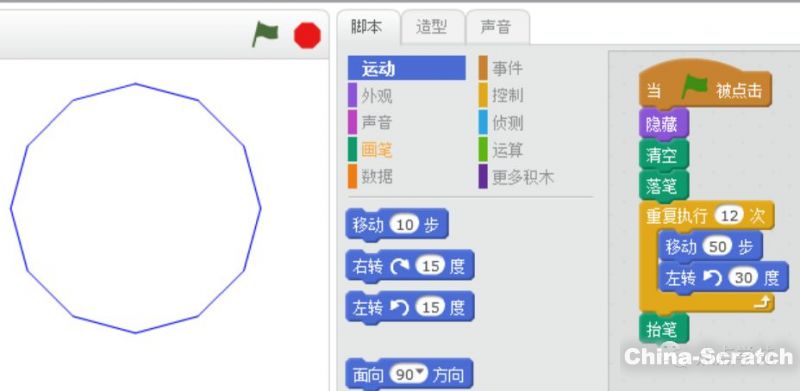
塞翁失馬,焉知禍福?我們本來想畫3條邊的正三角形,卻畫出了6條邊的正六邊形。如果我們把左轉(zhuǎn)的度數(shù)縮小一半到30度,把重復(fù)執(zhí)行的次數(shù)增加一倍到12次,看看能畫出個什么來呢?
當然了,畫過一次后,我們發(fā)現(xiàn)舞臺區(qū)不大,得把移動的步伐縮小點,不然又畫出去了。
?
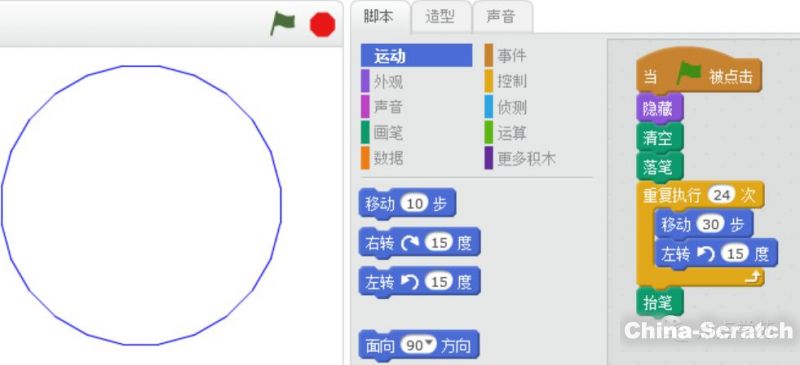
正二十四邊形
哈哈,繼續(xù),正二十四邊形都出來了,有沒有發(fā)現(xiàn)什么規(guī)律了嗎?
?
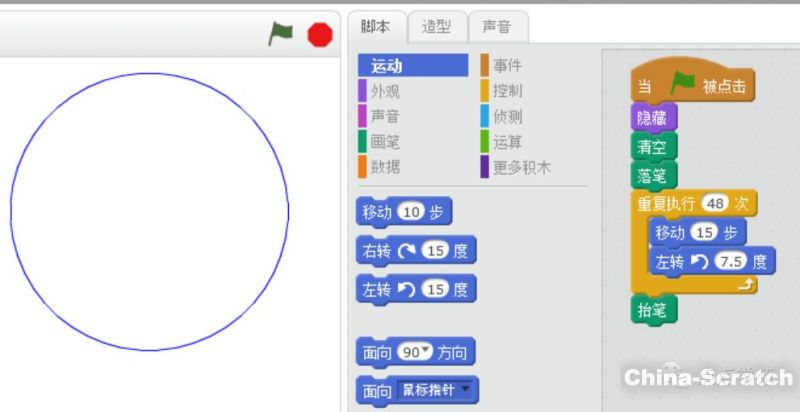
圓
明明是想畫正48邊形的,為什么看起來這么像圓?其實小朋友不知道的是,我們古時候的祖沖之呀,計算圓周率的時候,就是用這樣的割圓術(shù)去逼近圓的。當正多邊形的邊數(shù)越來越大的時候,畫出來的圖形,越來越接近于圓。
?
找規(guī)律
小朋友學(xué)數(shù)學(xué),要善于找規(guī)律。
我們畫了正六邊形、正12邊形、正24邊形、正48邊形,結(jié)合每次轉(zhuǎn)的角度,有沒有發(fā)現(xiàn)什么規(guī)律呢?
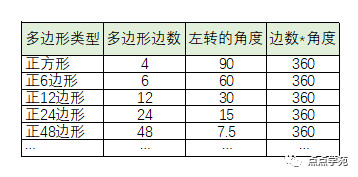
細心的小朋友可能還真發(fā)現(xiàn)了?我們把角度乘以邊的個數(shù),怎么乘積都是360度呢?
如果是正三角形,那3條邊,左轉(zhuǎn)的角度應(yīng)該是360/3=120度吧。
?
正三角形
還真是這樣,原來畫三角形的時候得左轉(zhuǎn)120度呢。
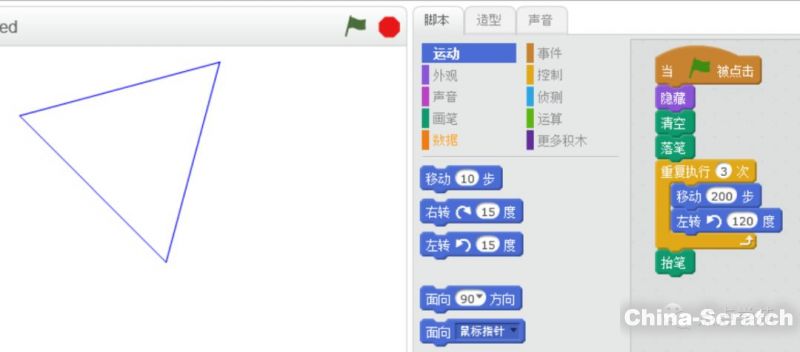
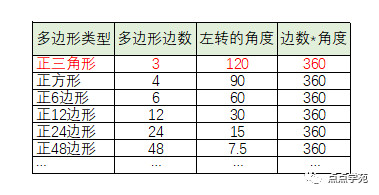
綜合上面所畫的正多邊形,其實我們發(fā)現(xiàn)了一個定理:
多邊形外角和等于360度
?
正N邊形
依賴于這個性質(zhì),我們就可以根據(jù)上面的腳本畫出任意正多邊形,譬如畫個正n邊形,那我們只要左轉(zhuǎn)360/n度就可以。
當然了,要控制下步數(shù),免得畫到“舞臺區(qū)”外面去了。
組合成動畫?知道了制作各類多邊形后,那我怎么依次把這些正多邊形畫個遍呢?
當然了,從上節(jié)內(nèi)容來看,多邊形邊數(shù)變大了,無非就是越來越像圓了,邊數(shù)大了后,憑我們的眼睛又看不出差別,所以啊,我們畫前面10多個正多邊形就好了。
那我們得想想,每次循環(huán)畫正多邊形的時候,多邊形的邊數(shù)是不是不斷變化的呢?這個要怎么實現(xiàn)?
?
變量
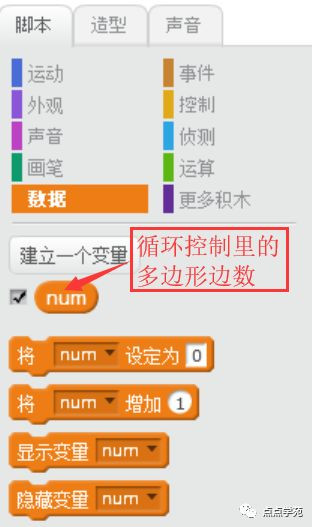
循環(huán)的時候不斷變化的值,我們可以存在變量里。
譬如,我們定義一個變量num,專門來存放正多邊形的邊數(shù)。
?
雙層循環(huán)控制
我們每次畫一個正多邊形num的時候,需要循環(huán)num次才能把該多邊形畫好,前面提到過,num變化的時候,我們也需要用一層循環(huán)來控制,那這樣就需要兩層循環(huán)來控制。
?
完整腳本
全部腳本如下所示:
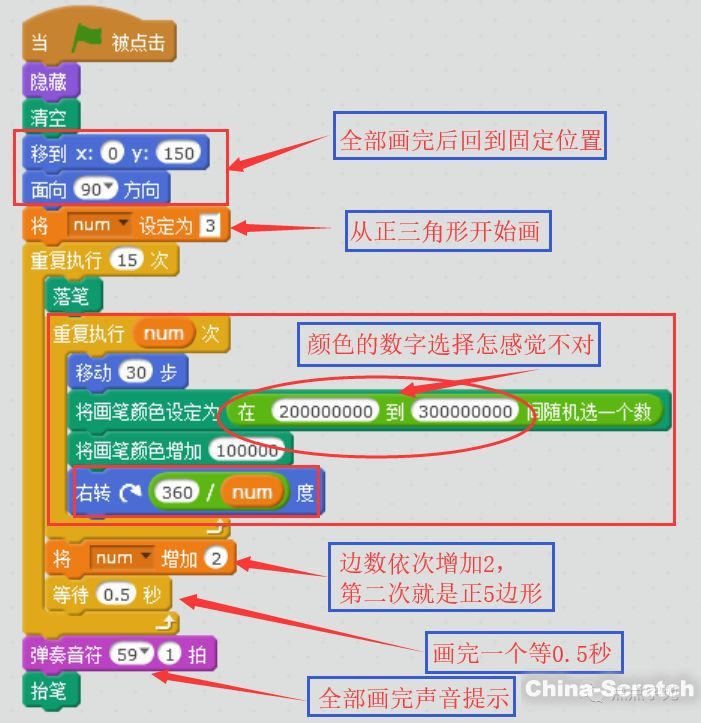
?
動畫效果圖
為了看起來不至于太單調(diào),每畫一邊的時候隨機設(shè)置了畫筆的顏色。
不知道大家有沒有發(fā)現(xiàn),前面這個五彩繽紛的動畫,有一個一直不變的東西,那就是正多邊形的邊長,我們每次循環(huán)畫邊的時候,移動的步數(shù)都是30步吧。
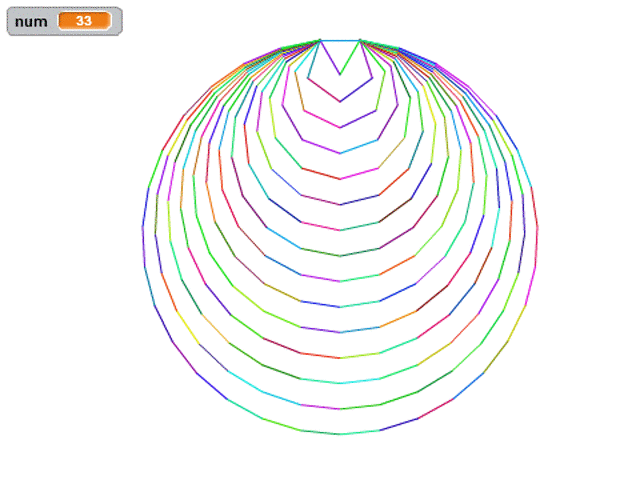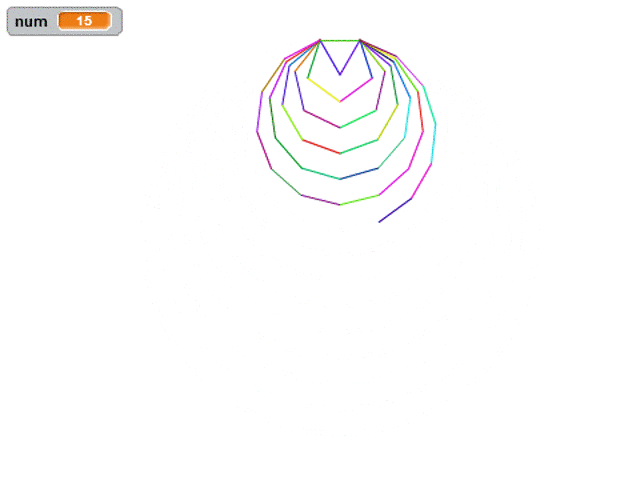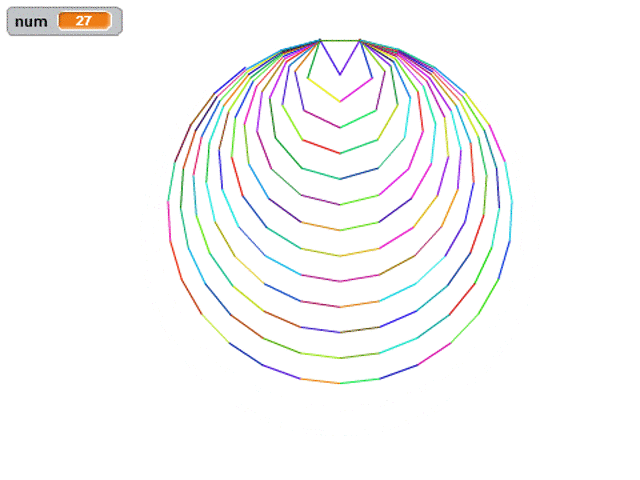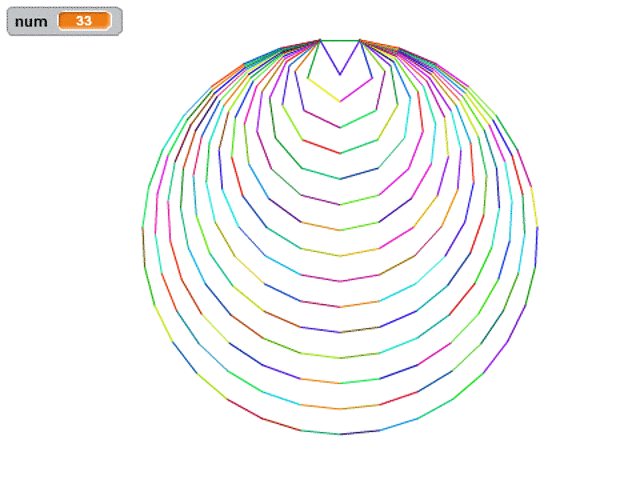
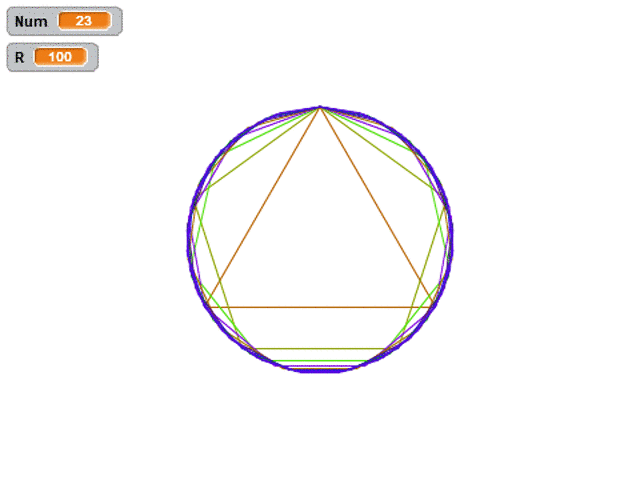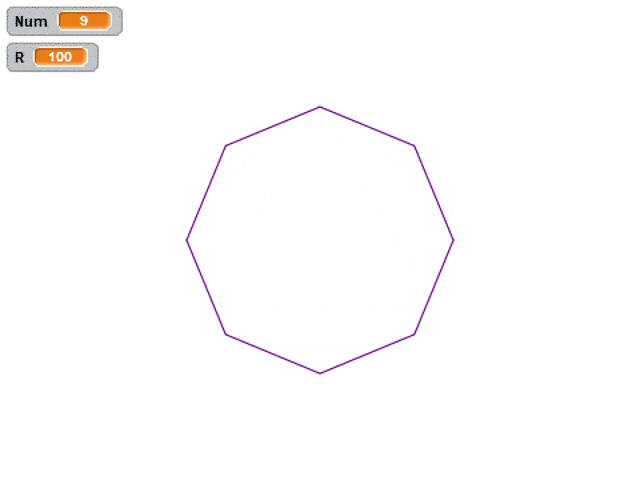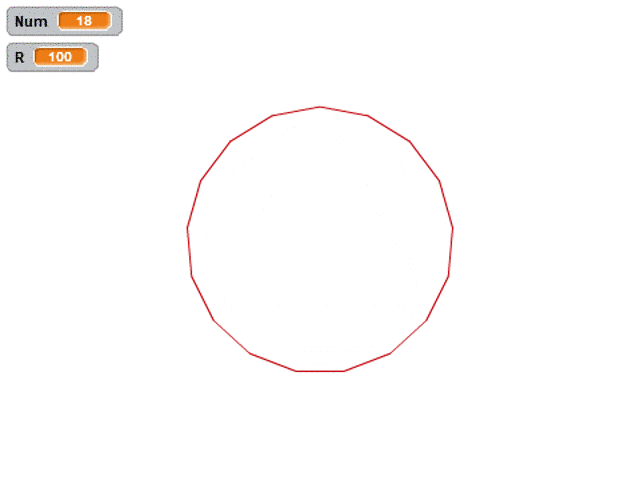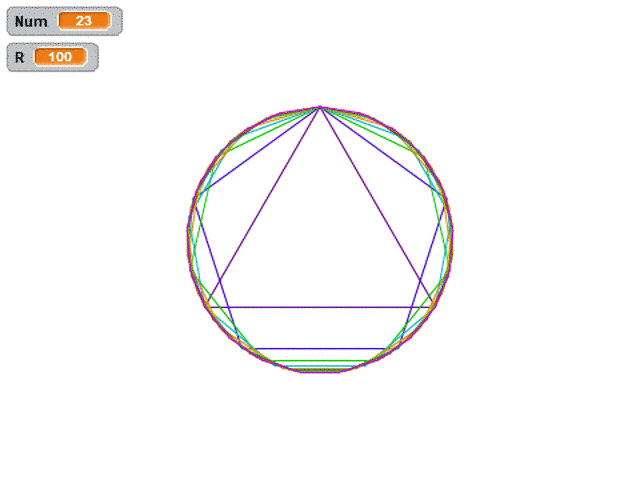
那我們現(xiàn)在換一種方式,我們繪制所有的正多邊形,外接圓都重合的話要怎么畫呢?
什么叫外接圓重合呢,每個正多邊形的頂點共圓,我們要讓所有多邊形的頂點都在同一個外接圓上。
那這些正多邊形之間有哪些共同的特性呢?
?
不變的常量——外接圓半徑
所有正多邊形中,從圓心到任意一個多邊形的端點,也就是圓的半徑,一直是不變的。
還記得前面做的那個動圖,不變的是什么嗎?不變的是邊長。
為了方便在腳本里編寫調(diào)試,我們將這個不變的半徑設(shè)置成一個常量R。當然,在scratch里其實都是變量。
我們將邊數(shù)也設(shè)置成一個變量Num。

?
固定出發(fā)點,調(diào)整好繪制方向
為了方便繪制,我們計劃所有的正多邊形統(tǒng)一從坐標系中的某個點出發(fā),譬如坐標系中的點E{x=0,y=R}。
在scratch中,我們每次繪制一個正多邊形的時候,都要將位置移動到{0,R}這個點,然后面朝某個方向開始繪制。
而對于正Num邊形來說,這里我們?nèi)um=6,也就是我們以正六邊形為例。當我們把位置移動到{0,R}的時候,第一條線繪制的方向是不是線段DE的方向呢?
最初我們從圓心O{0,0}往上移動到E{0,R}的時候,是朝正北的,到了E點后,要轉(zhuǎn)向到ED的方向,如下圖所示:
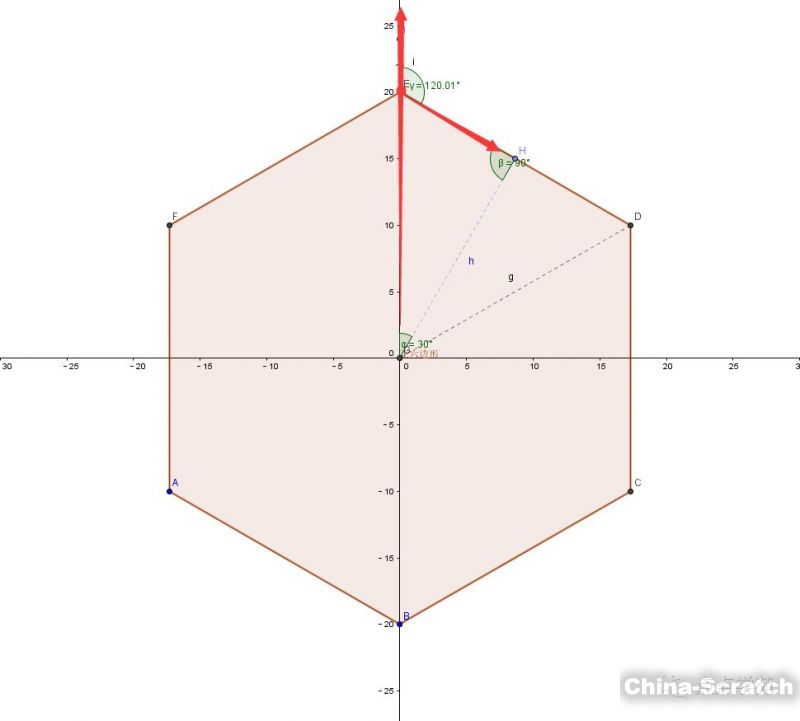
通過上個動畫的制作,我們知道所有正多邊形的外角和是360度,所以每個正多邊形的內(nèi)角是180-360/Num,所以從OE轉(zhuǎn)向DE,線段要面向的方向是180-(180-360/Num)/2=90+180/Num。對于正六邊形來說,就是要面向120度的方向。
?
邊長
在六邊形中,我們確定好起點E和方向后,我們還有確定好線段ED的長度。
其實,我們很容易知道角HOE為360/Num/2=180/Num。
根據(jù)正弦定理,易知線段EH=R*sin(180/Num),所以線段DE的長度就是線段EH的兩倍,也就是2R*sin(180/Num)。
?
右轉(zhuǎn)方向
線段ED繪制好了以后,我們從線段ED轉(zhuǎn)向線段DC,右轉(zhuǎn)的度數(shù)是不是一個外角那么大呢?外角和是360度,那這個外角就是360/Num。
那這樣循環(huán)Num次,正Num邊形是不是畫好了呢?
?
完整腳本
完整腳本如下所示:
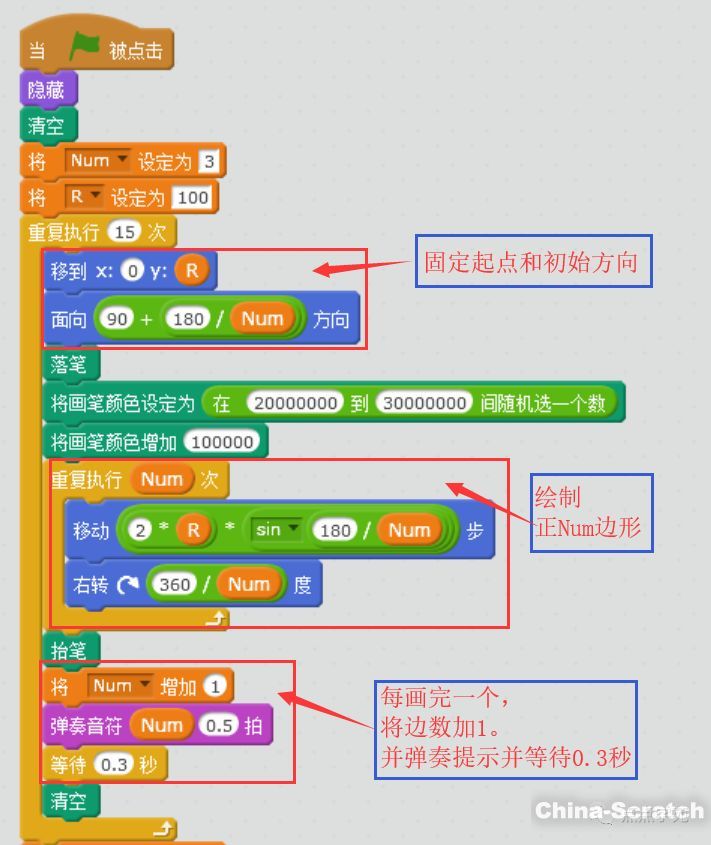
完整效果圖如下,和前面的視頻相比,只是增加了隨機色而已。
聲明:本文章由網(wǎng)友投稿作為教育分享用途,如有侵權(quán)原作者可通過郵件及時和我們聯(lián)系刪除